Ancient Greece

Athens was One of Many Ancient Greek Poleis (plural for Polis [city-state] "Metropolis") a Civilization and Culture so Rich that they had Pondered Ideas beyond their own Imagination. The contributions of the Atheneans and related cultures such as Indo-Arabic, Mesopotamian, Babylonian, Egyptian and later Western Influence has and forever will be seen (by Historians & Scientists) as the Greatest Civilization to Exist. This $\textit{Garden of Eden}$ has its Roots in the Archipelago right off the East coast of Greece, which you can see on the map below:

During a later stage of the Greek civilization, Greece (a network of towns${}^{1}$; see this list) was referred to by many as Ε λ λ α ς [Hellas] (the place of the Hellenists - a culture of people who were mainly worshipers of the sun (Hellios), oceans (Poseidon) and other universal elements. They understood that there were other sources of energy and interaction of elements in our physical realm that nurture interesting relationships to our understanding of it, distinct from our own minds.

${}^{1}$A network of towns: due to the expansion of the trading canal in the Mediterranean Sea

Their choice of religion was heavily influenced by the Egyptian Calendar System for optimizing their harvests during the agricultural farming process. The Hellenists became known for sharing and collecting knowledge & secrets of the world. Fame and Brilliance of Philosophers such as Plato, Euclid, Archimedes, etc. are widespread and had an influential impact on the Ancient Greek civilization, as a culture. This in turn stimulated scientific enquiry in multiple disciplines to investigate phenomena in their respective fields of research. In science, we often attempt to predict certain aspects of physical reality using our capacity for reasoning and observation. Modern day humans do science for much the same reason as did the Ancient Greeks: $$\text{Activity for Leasure & Practical Purpose}$$

for the sake of

$$\text{"discovering something new"}$$

The analysis of thought, reasoning & arguments as well as debate & dialogue was a widely & wildly popular activity during the peak of the Athenean culture, especially in their doctrines, where they strived to become more civilized. Hence, the Atheneans were extremely motivated to formalize arguments and systematize reasoning, so as to be able to conclusively decide what is "right" versus what is "wrong". The Atheneans had already largely implemented the ideas of Democracy in Politics, Gymnasia in Athletics, etc. It is evident that Law, Religion, Mathematics, Music and many other disciplines played an important role in shaping the early developments of Philosophy as a whole. Today it is used to implement new ideas in Artificial Intelligence & Machine Learning to be encountered in later chapters of this article.

Language

Mathematics, like English, is a language, however more sophisticated. It is often described as the language of science, but is more appropriately characterized as the language of ideas.

All languages have an alphabet, which consists of a group of letters that are used to make words. Words are then used to make phrases. Phrases can be combined to produce statements & propositions. There are also rules of grammar which explain how words are joined together. Punctuation such as parentheses, braces, brackets, commas & other symbols are further used to clarify meaning & understanding.

Mathematical language is expressed in a complex, but very precise way, which does have some similarity to any natural language. Mathematics, at its core, relies on "ordinary" language, logic & a wide range of precisely defined conventions, notation, symbols, graphical & abstract representations, operations and detailed statements.

Like any natural language, mathematics also has letters which include numbers, variables, parameters & symbols that are used as placeholders, coefficients, indices, operations, relations & connectives, which constitute statements, terms, expressions, equations etc. Perspective is further provided by declaring interpretation of symbols.

Semantics is the linguistic & philosophical study pertaining to meaning & interpretation while syntax refers to grammar or set of rules that must be applied to join symbols, words & phrases for creating well-formed sentences. A bunch of symbols that are grouped together doesn’t necessarily make a sentence. For example, the string of characters

“My! running & every? focus very, (and”

conveys no meaning. The above string of characters lacks both syntactic & semantic essence.

In fact, it is rather nonsensical, completely confusing to the reader & resembles information from a corrupt database. Hence, certain criteria govern how symbols and words can and cannot be compiled into a sentence to synthesise meaning. In the spirit of mathematics, it is pointless to write

"$ − ( + 4 \times 3 x + \sqrt{+} . ^2 $"

It is exaggeratingly ridiculous to utter symbols in an uncontrolled fashion.

Syntax can also influence the semantic aspects of statements. Consider the comparative sentences below:

“Aristotle says he wants to please only the King“
“Aristotle says he wants only to please the King”
“Only Aristotle says he wants to please the King”

Each of the sentences above contain the same word elements but convey completely different meaning, due to the variation in syntactical usage of the word ‘only’. In mathematics, syntax works a little differently, sometimes it is true that the order in which expressions are joined together doesn’t matter. Other times it is of equal importance that the order is specificied. A simple example is the assertion that 2 + 3 produces the same result as 3 + 2, however 2 - 3 is distinct from 3 - 2. This is due to the commutative nature of the addition operation.

Mathematics places great emphasis on the ability to write clearly & concisely, and, above all, unambiguously. Roughly speaking, mathematical notation is intended to condense everyday language & thought into powerful symbols that can be readily manipulated using arithmetic.

In language, the fluency of communication depends on the ability to exchange abstract ideas effectively & recognizably. Argumentation entails the process of convincing an audience via presentation & justification of reason in support of an idea. Reasoning relies on establishing the truth of statements, which can then be used to build up a chain of thought leading to a conclusion.

This might seem obvious to us now, but the idea of constructing a rational argument distinguishes philosophy from the superstitious and religious explanations that had existed before the first scientific theories. Philosophers had to devise a way of ensuring their ideas had validity. What emerged from their disciplines was logic, a technique of reasoning that was gradually refined over time. At first, simply a useful tool for analysing whether an argument "held water", logic developed rules and conventions, and soon became a field of study in its own right, another branch of the expanding subject of philosophy.

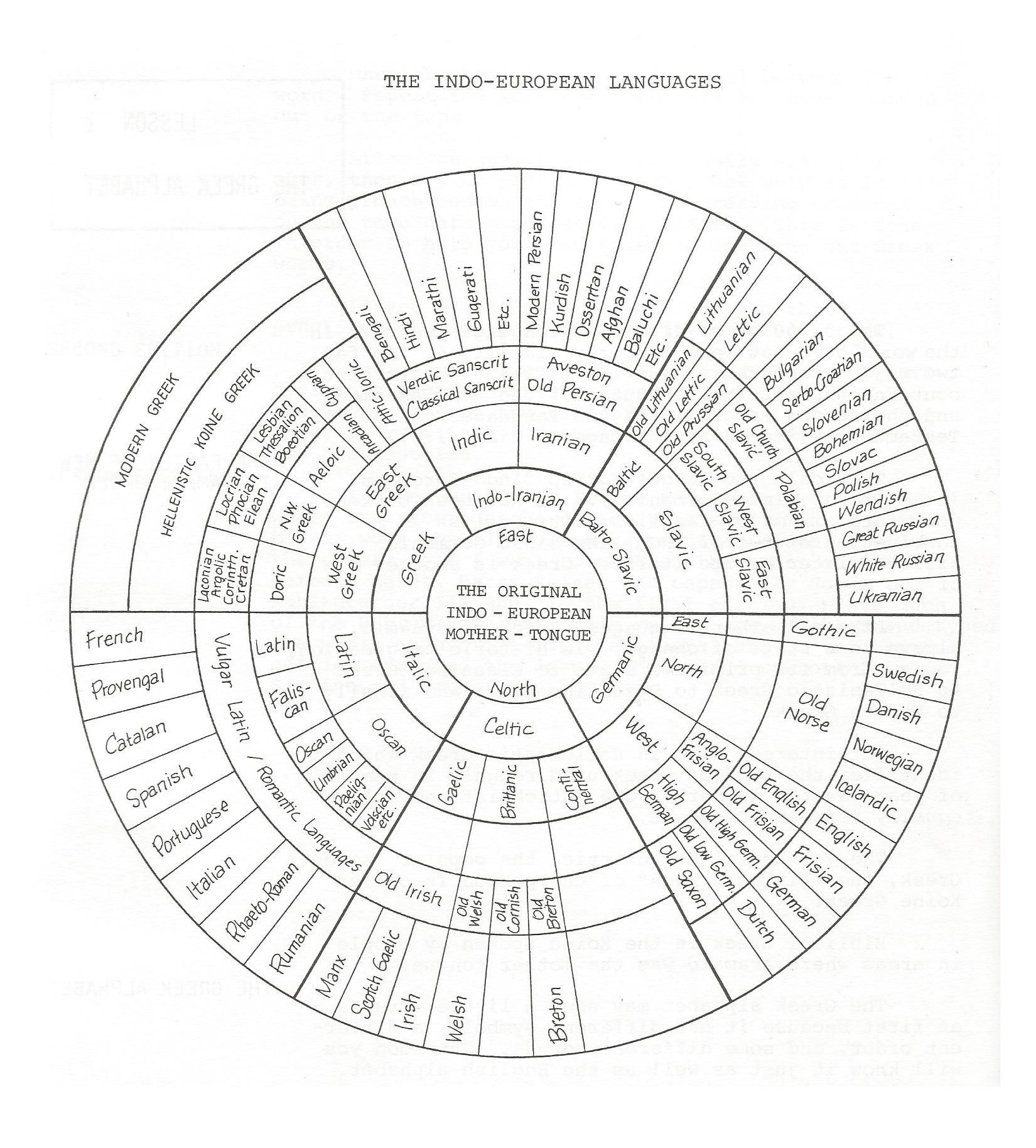
Like so much of philosophy, logic has intimate connections with science, mathematics & computer science. The basic structure of a logical argument, starting from a premise and working through a series of steps to a conclusion, is the same as that of a mathematical proof. It’s not surprising then, that philosophers have often turned to mathematics for examples of self-evident, incontrovertible truths, nor that many of the greatest thinkers, from Π υ θ α γ ó ρ α ς (Pythagoras) to $\mathscr{R}$ené $\mathscr{D}$escartes & $\mathcal{G}$ottfried $\mathcal{W}$ilhelm $\mathcal{L}$eibniz, were also accomplished mathematicians.

Although logic might seem to be the most exact branch of philosophy, a discipline in which statements are either "right" or "wrong", a closer look reveals that it is not so obvious. Advances in mathematics in the 19${}^{\text{th}}$ century called into question the rules of logic that had been laid down by Α ρ ι σ τ ω τ ε λ η ς (Aristotle), but even in ancient times, Ζ η ν ω ν   ó   Ε λ ε α τ η ς's (Zeno of Elea's) famous paradoxes reached absurd conclusions from apparently faultless arguments.

A large part of the problem is that philosophical logic, unlike mathematics, is expressed in words rather than symbols, and is subject to all the ambiguities and subtleties inherent to natural language. Constructing an argument involves using language carefully and accurately, examining statements and arguments to ensure that

we say what we mean & we mean what we say

Terminology

Metalanguage

Metalanguage pertains to the discourse of the philosophical discussion at hand in an investigatory and interjectory manner.

Formal System

A formal system or frame of calculus (proposed by $\mathcal{D}$avid $\mathcal{H}$ilbert in 1921) serves as the environment in which to perform the arithmetic of logical rules of inference.

Definition

A definition is an exact description of an object or explanation of a concept.

For example, in geometry we may define a point as a (geometrical) object having no dimensions

Proposition

A sentence that can be labelled true or false, is a statement or proposition. Several propositions can be combined to produce a larger composite proposition.

Predicate

A predicate can be understood as the property that an object adheres to or is characterized by, which is inherent to an element.

For example, in the statements the grass is always greener on the other side, green-ness is predicated upon the grass.

Postulate/Axiom

A(n) axiom or postulate is a statement that is self-evident in nature, regardless of justification. It is a supposition from which a theory is built and does not need to be proved.

For example, the statement lines that are not parallel, intersect in exactly one point is accepted as true & cannot be proved.

The words axiom & postulate mean the same thing but are used in disjoint historical contexts.
Postulate is mainly used in the disciplines of Geometry and Physics whereas axiom is generally used in Mathematic.

Premise/Hypothesis

A premise or hypothesis is a proposition in the form of an assumption or a true statement, on which reasoning proceeds in support of an argument or proof.

Theory

A theory is a system of organized axioms/postulates & definitions within the discourse of a subject matter that produce more insightful results. These results deduced from this body of discourse are called theorems.

An example of a powerful set of postulates/axioms & definitions that gives rise to a theory includes Euclidean Geometry

Theorem

A theorem is an interesting result that has been proved by a combination of postulates/axioms & definitions.

For example, the theorem tangent lines that intersect at a point are congruent can be derived from Euclid's postulates of Geometry.

Conjecture

A conjecture is a statement suspected to be a theorem but is yet to be proved

Corollary

A corollary is a statement that follows easily from a previous result, often a special case of a theorem.

An example of a corollary to the theorem the angle subtended at the centre of a circle is double the angle at the circumference could be the statement that the diameter subtends a right angled triangle at the circumference

Lemma

A lemma can be considered as a helping theorem or minor theorem, used as a stepping stone to a larger result rather than as a statement of interest itself, without having to dwell off course of the discussion at hand.

Connectives

In English there are more than one way in which words, phrases and expressions can be joined together. This is achieved by using connective words. Connective words that are commonly used to join sentences include “and”, "or", “but”, “although”, “while”, “unless”, “after”, “because”, “therefore”, etc. Connectives merge words and phrases into a single expression. Depending on the connective used, it can determine condition, combination or generally coordinate the meaning of phrases.

In classical logic, connectives have rough equivalents to that of natural language. Connectives are used to combine propositions in a specific way & assign a truth value to an argument form.

Negation (not ...)

not (#)

$\neg$ (#)

$\neg$ [proposition]

Negation is a unary connective, which means that it takes only one proposition as argument.

Conjunction (... and ...)

(#) and (*)

(#) $\land$ (*)

[proposition 1] $\land$ [proposition 2]

Conjunction is a binary connective, which means that it takes two propositions as argument.

Disjunction (... or ...)

(#) or (*)

(#) $\lor$ (*)

[proposition 1] $\lor$ [proposition 2]

Disjunction is a binary connective. Clasically, its intended interpretation is inclusivity, which means that if either proposition 1 or proposition 2, or both proposition 1 and proposition 2 are true, then their combined argument form is also true.

Implication (if ... then ...)

if (###) then (***)

(###) $\rightarrow$ (***)

Implication is a binary connective. The condition is usually called the antecedent while the conclusion is called the consequent.

[condition] $\rightarrow$ [conclusion]

Bi-implication (... if and only if ...)

(###) if and only if (***)

(###) $\leftrightarrow$ (***)

[proposition 1] $\leftrightarrow$ [proposition 2])

Bi-implication is a binary connective. In metalanguage, this connective is often abbreviated as "iff".

Quantification

The Principle of Universal Quantification

The Principle of Universal Quantification suggests that a certain property is true for all elements in a set.

For example, the satement that the square of any number is positive can be expressed in First Order Logic as $\forall x \space (x^2 \geq 0)$

The Principle of Existential Quantification

The Principle of Existential Quantification suggests that there is at least one element in a set having a certain property.

For example, the statement that there is a prime number that is even can be written in First Order Logic as $\exists x \space (x \in \text{the set of all prime numbers} \land x \in \text{the set of all even numbers})$

Statement Forms

Statements can be expressed in various forms. These different forms of a statement can reveal important insights about the original statement, or serve as a technique to prove otherwise impossible or complicated statements.

Given the hypothesis if P, then Q. We can create three related statements:

Statement	Form	Symbolic
Hypothesis	If P, then Q	$P \rightarrow Q$
Converse	If Q, then P	$Q \rightarrow P$
Inverse	If not P, then not Q	$\neg P \rightarrow \neg Q$
Contrapositive	If not Q, then not P	$\neg Q \rightarrow \not P$

Example:

Designate by M the predicate you eat MacDonald’s
Designate by F the predicate you are fat

The statement $M \rightarrow F$ can be interpreted as if (you eat MacDonald’s), then (you will become Fat)

Converse

The converse of the statement above is written as $F \rightarrow M$ and can be interpreted to mean that if (you are Fat), then (you have eaten to much MacDonald’s)

Inverse

The inverse of the statement above is written as $\neg M \rightarrow \neg F$ and can be interpreted to mean that if (you have not eaten too much MacDonald’s), then (you are not fat)

Contrapositive

The contrapositive of the statement above is written as $\neg F \rightarrow \neg M$ and can be interpreted to mean that if (you are not fat), then (you have not eaten to much MacDonald's)

Properties

The contrapositive of a statement is the converse of the inverse of the statement.

If a statement is true, then its contrapositive is necessarily true.

If a statement is true, the converse is not necessarily true, for example, the statement if (you are fat), then (you have eaten to much MacDonald's) is not necessarily true, since it could be the case that you have eaten to much KFC

Example:

Designate by R the predicate the quadrilateral is a rectangle
Designate by P the predicate the quadrilateral has two pairs of parallel sides

The statement $R \rightarrow P$ can be interpreted as if (a quadrilateral is a rectanlge), then (it has two pairs of parallel sides)

Converse

The converse of the statement above is written as $P \rightarrow R$ and can be interpreted to mean that if (a quadrilateral has two pairs of parallel sides), then (it is a rectangle)

The above statement is obviously false, since it could be that the quadrilateral is a parallelogram.

Inverse

The inverse of the statement above is written as $\neg R \rightarrow \neg P$ and can be interpreted to mean that if (a quadrilateral is not a rectangle), then (it does no have two pairs of parallel sides)

Contrapositive

The contrapositive of the statement above is written as $\neg P \rightarrow \neg Q$ and can be interpreted to mean that if (a quadrilateral does not have two pairs of parallel sides), then (it is not a rectanlge)

Proof Techniques

Sometimes a statement is simple, other times it is complex. But whether a statement is straightforward or complicated, it can only be accepted as true if it is proven. If you are uncertain about a certain fact, it is in your best interest to do research and gather enough information from which you can draw a conclusion. This will give you the sense of conviction of an argument. The method of producing such conclusion is called proof and the process is the derivation of such a fact.

(Formal) Proof

A (formal) proof is a sequence or list of statements (axioms/postulates & definitions) organized/structured in such a way to establish the truth of a conclusion. It is a step-by-step argument in which each statement is logically valid and in which each statement in aim of the conclusion is accompanied by a reason. The correctness of a proof depends on the validity of the steps taken, leading to the conclusion. Each statement is written on the left hand side of the page and the accompanying reason is written on the right hand side of the page in the same line as the statement which it supports. To round off a proof, the conclusion of the proof is expressed explicitly, followed by the letters Q.E.D. which is an abbreviation of the Latin phrase “Quod erat Demonstrandum” which means “what was to be demonstrated”.

Direct Proof

This is a proof in which all the statements used are true in its natural order or straight forward way, and all arguments are valid. Sadly, this is the only technique explored in undergraduate mathematics courses.

Proof by Contradiction/Reductio ad Absurdum/Indirect Proof

This is a Proof in which one assumption is made in such a way that, using valid arguments, a false conclusion is arrived at, which contradicts the assumption, inferring the opposite of the assumption is true.

Proof by Exhaustion

This is a technique which can only be applied to arguments with restrictive conditions. It entails justification of each particular case of a statement, which is established by working through every possible case & finding no contradictions, eliminating impossibilities, one case at a time.

Proof by Induction

This is a technique consisting of two stages. The first stage of the proof requires verification of the base case. The second stage of the proof requires verification of the resulting cases after assuming the inductive hypothesis. From this action, it follows that all cases are true.

Constructivist versus Classical/Non-Constructivist Mathematics

In the philosophy of mathematics, Constructivism asserts that it is necessary to find or construct a specific example of a mathematical object in order to prove that an example, adhering to a particular property, actually exists. Contrastingly, in classical mathematics, one can prove the existence of a mathematical object without specifically finding such a particular object explicitly, by assuming its non-existence and then deriving a contradiction from that assumption. A proof of the existence of such a mathematical object might be called non-constructive & a constructivist might reject it. The constructive viewpoint involves a verificational interpretation of the Existential Quantifier $\exists$, which is at odds with its classical interpretation.

Philosophy

Riddles

A riddle is a type of question posed in a complex way anticipating a clever response. Riddles are problems that can be solved by means of logical arguments. The word riddle is derived from the same root as ‘rider’ (often used in Geometry) which refers to a mathematical problem.

Below we present some interesting Riddles

1. A girl was ten years old on her last birthday and will be twelve years old on her next birthday. How is this possible?


2. Two fathers and two sons go fishing. They each catch a fish for the day. They bring home three fish. How is that possible?


3. A father and his son was involved in a vehicle collision. The father died while the boy was rushed to emergency surgery. On entering the operating theatre, the surgeon cried “I cannot operate on this boy because he is my son.” How is this possible?


4. In a father’s will, he stated that his two sons must race their horses for inheritance. “The son with the slowest horse will receive my entire fortune”. The two sons race but never finish, as they deliberately slow their horses. After visiting the Oracle, they race their horses at full speed. What was the Oracle's advise?

Solutions:

1. It is currently the girl’s birthday
2. A grandfather, his son and his grandson each caught a fish
3. The surgeon is the boy’s mother
4. The Oracle told them to swap horses

Paradox

A paradox is a statement that, despite apparent sound reasoning from true premises, leads to a self-contradictory or a logical inconsistent conclusion.

Are the following statements true or false?

1. I’m a compulsive liar
2. The following sentence is true
3. The previous sentence is false

The statements above are inconclusive, i.e. it is impossible to determine whether they are true or false. This illustrates a form of circular reasoning. These type of statements are called paradoxes.

There are also other paradoxes which are indicative of the limitations of our tangible realm. Zeno of Elea’s famous paradoxes include Achilles and the Tortoise and the Arrow which all indicate the restricted capacity of our mind to comprehend certain aspects of the physical world. Only with the recent development of Quantum Physics & extreme efforts within logic, these paradoxes are starting to unravel.

Achilles and the Tortoise

Assume that space and time is infinitely divisible. If Achilles is at $A$ and the tortoise is at $B$, then Achilles can never catch the tortoise, since by the time Achilles reaches $B$, the tortoise will be at some further point $C$, and by the time Achilles reaches $C$, the tortoise will be further ahead at $D$, and so on ad infinitumm, thus the tortoise will always be ahead of Achilles.

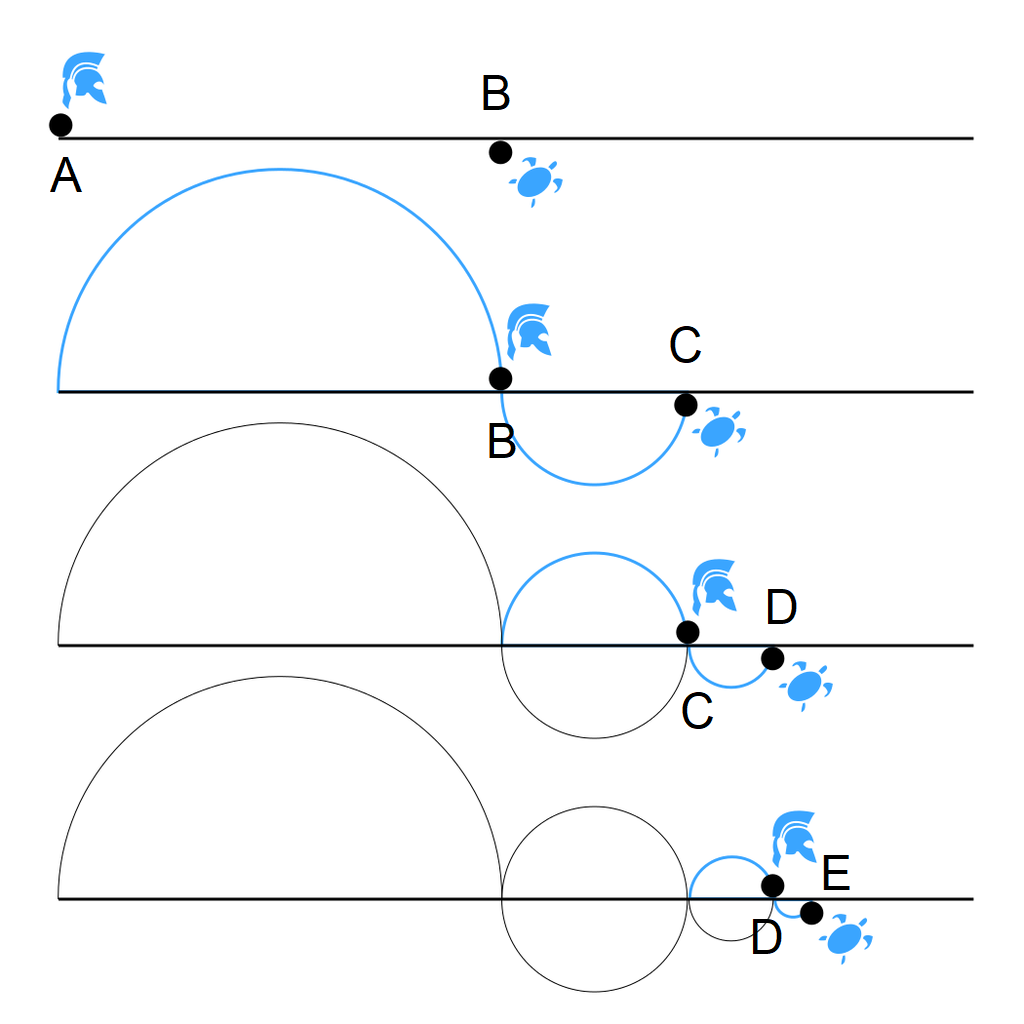
Zeno's Arrow

Assume space and time are not infinitely divisible. Hence, there is an indivisible smallest unit of space (a point) and an indivisible smallest unit of time (an instance). If you shoot an arrow using a bow, the arrow must be at a given point at a given instance. Since the arrow cannot be in two places in the same instance, it cannot move in that instance, so it remains in that instance, therefore the arrow is stationary.

For each of the paradoxes above, we find ourselves in a dilemma. The assumption from Achilles and the Tortoise and the Arrow lead to absurd conclusions and contradict common sense, therefore they are paradoxical.

Bertrand Russel's Barber Paradox

If the barber is the one who shaves all those, and those only, who do not shave themselves, does the barber shave himself?

The Laws of Thought

The Laws of Thought listed below are fundamental axiomatic rules upon which rational discourse is based. These rules are fundamental in the sense that they are the simplest, accepted set of rules on which an argument should be based. These are also the rules which are widely accepted to be true in the traditional/classical sense.

Axiom	Logic	Set Theory
1. Law of Identity	$A \rightarrow A$	$A \supset A$
2. Law of Exlcluded Middle	$ \neg A \lor A$	$A \cup X \setminus A $
3. Law of (Non-)Contradiction	$ \neg (A \land \neg A) $	$ A \cap (X \setminus A) = \emptyset $

Αριςτοτελησ was the one who came up with the ideas of what may be important axiomatic assumptions from which all truths can be derived. The modern approach to reasoning is not necessarily so straight forward and may question or even reject some or all of The Laws of Thought listed above. We will investigate these laws one at a time to better clarify and understand their significance. The study of such rules have a long tradition in the history of philosophy and logic and extends to the modern ideas of computer science.

1. The Law of Identity

The Law of Identity states (in simple English) that "whatever is, is". This may be represented symbolically using logical symbols:

$$ A \rightarrow A $$

An alternative notation to express The Law of Identity makes use of the symbols of set theory:

$$ A \supset A $$

The notation $A \supset A$ above, is due to $\mathcal{G}$iuseppe $\mathcal{P}$eano and is interpreted to mean that $A$ is a subset of $A$. For someone familiar with only the basics of set theory, this expression seems "backwards" but is, in fact, intentionally written this way to emphasise it's connection to the arrow (implication) notation.

2. The Law of Excluded Middle

The Law of Excluded Middle is usually voiced in Shakespearen literature by the phrase ":to-be;;or;;not:to-be" and states that for every proposition, either this proposition or its negation is true. symbolically:

$$\neg A \lor A$$

Alternatively, we can express The Law of Excluded Middle using the notation of set theory:

$$A \cup X \setminus A$$

The Law of Excluded Middle is appropriately named since it establishes that there is no in between, when it comes to "right" or "wrong".

3. The Law of (Non-)Contradiction

Obviously, two contradictory statements cannot both be true, so we take it as a "law". Symbolically, we can represent this with the expression:

$$\neg (\neg A \land A)$$

If we wanted to express this law using the symbols of set theory, we would represent this with the expression:

$$(A \cap X \setminus A) = \emptyset$$

That is to say that $A$ and its complement $X \setminus A$ has nothing in common, i.e. their intersection is the empty set $\emptyset$.

Bivalence, Duality & Complementation

The Principle of Bivalence states that any declarative sentence expressing a proposition has exactly one truth value, either true or false. A system satisfying this principle is called a bivalent or two-valued system.

From our previous discussion about The Laws of Thought, we observe that The Duality Principle is "built into" our system of reasoning in the sense that we reserve the capacity to distinguish a certain event from its (complementary) dual. The Duality Principle arises naturally in many mathematical settings and is usually associated with some sort of symmetric phenomena, closely related to the complement of a mathematical object, in the sense that an object together with its complement forms the whole.

$\mathcal{S}$herlock $\mathcal{H}$olmes enunciated that

"if you eliminate the impossible, however improbable, what remains, must be the truth".

This is suggestive of The Duality Principle, that one or the other must be the case, but not both. The Duality Principle is relevant in contexts of other mathematical theories as well, such as in Probability Theory, Graph Theory, Abstract Algebra, Linear Algebra, Functional Analysis, Topology, the list goes on ...

Tautologies

It may become apparrent later on that The Law of Identity & The Law of Excluded Middle are equivalent, i.e. $A \rightarrow A \equiv \neg A \lor A$. It may already be apparent to the reader that the expressions for The Laws of Thought are, in fact, what we call, Tautologies, which is a statment that is true regardless of context. A Tautology is true, based merely on the syntactic argument form, rather than the interpretation or meaning of the statement itself.

Expressive Power

Can we really derive all truths from The Laws of Thought? This seems like a Question for the Gods, but in fact, we learn that the answer is trivially disappointing! We need more expressive power over objects to build a strong basis for reasoning with cour classical rules of inference. For this purpose we introduce the set of connectives $\{ \neg, \land, \lor, \rightarrow, \leftrightarrow \}$ borrowed from classical logic. $\mathcal{G}$eorge $\mathcal{B}$oolos is often credited as being the first analyst to algebrize logic in an attempt to reduce all of mathematical reasoning to a set of connectives/operators. $\mathcal{G}$otlob $\mathcal{F}$rege generalized the work of $\mathcal{G}$eorge $\mathcal{B}$oolos a step further by introducing the Principles of Existentiality $ \exists $ & Universality $ \forall $ for Quantification in mathematical discourse, thus extending the expressive power of Propositional Calculus to what is today referred to as Predicate Calculus.

While maintaining expressive power over precise mathematical statements, we prefer to use a minimal number of symbols to reduce unnecessary work required to develop the theoretical discourse of our formal system of reasoning all the while preserving the breadth of ideas that can be encapsulated by our language. A formal system adhering to this property is described as being Functionally Complete or Adequately Expressive.

Interpretation

An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics.

List of Prominent Philosophers

Throughout the timeline of logic, the ability to capture the pure concept of reasoning serves nearly impossible. Many great scholars throughout history have devoted their efforts to systematize thinking. Below is an exhaustive list of some the most prominent philosophers, scientists, logicians, mathematicians & physicists of all time, together with a short account of their contributions towards modern computer science up to and including the 21$^{\text{st}}$ century.

Π υ θ α γ ó ρ α ς   ó   Σ α μ ι ο ς   (c. 570 - c. 495 BC)   [  Magna Gracia  ]

Η ε ι ρ α κ λ ε ι τ η ς   (c. 535 - c. 475 BC)   [  Ε φ ε σ ω ς  ]

Ζ η ν ω ν   ó   Ε λ ε α τ η ς   (c. 495 - c. 430 BC)   [  Magna Gracia  ]

Σ ω κ ρ α τ η ς   (c. 470 - c. 399 BC)   [  Athens - Capital of Greece  ]

Π λ α τ ω ν   (c. 423 - c. 348 BC)   [  Athens - Capital of Greece  ]

Α ρ ι σ τ ω τ ε λ η ς   (c. 384 - c. 322 BC)   [  Stagiro - Northern Greece  ]

Ε υ κ λ ε ι δ η ς   (c. 325 BC)   [  Egypt - Alexandria  ]

Α ρ χ ι μ η δ η ς   (c. 287 - 212 BC)   [  Syracuse - Sicily  ]

أبو يوسف يعقوب بن إسحاق الصبّاح الكندي   Abū Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī   (c. 801 - 873 AD)   [  Kutu/Baghdad  ]

$\Phi$ibonacci   (1170 - 1240)   [  Italy, Pisa  ]

秦九韶   Qin Jiushao   (Ch ' in Chiu-shao)   (c. 1202 – 1261)   [  Ziyang Sichuan  ]

$\mathscr{R}$ené   $\mathscr{D}$escartes   (c. 1202 – 1261)   [  France  ]

$\mathcal{J}$ohn   $\mathcal{N}$apier (1 Feb 1550 - 4 Apr 1617)   [  Scottish  ]

$\mathscr{G}$alileo di $\mathscr{V}$incenzo   $\mathscr{B}$onaiuti de' $\mathcal{G}$alilei (15 Feb 1564 - 8 Jan 1642)   [  Italian  ]

$\mathcal{C}$arl   $\mathcal{G}$ustav   $\mathcal{J}$acob   $\mathcal{J}$acobi (27 Dec 1571 - 15 Nov 1630)   [  German  ]

$\mathscr{B}$laise   $\mathscr{P}$ascal   (19 Jun 1623 – 19 Aug 1662)   [  France  ]

$\mathcal{R}$obert   $\mathcal{B}$oyle   (25 Jan 1627 - 31 Dec 1691)   [  Anglo-Irish  ]

$\mathcal{C}$hristiaan   $\mathcal{H}$uygens   (14 Apr 1629 - 8 Jul 1695)   [  Dutch  ]

$\mathcal{R}$obert   $\mathcal{H}$ooke   (18 Jul 1635 - 3 March 1703)   [  British  ]

$\mathscr{I}$saac   $\mathscr{N}$ewton   (25 Dec 1642 – 20 March 1727)   [  Britain  ]

$\mathcal{G}$ottfried   $\mathcal{W}$ilhelm   $\mathcal{L}$eibniz   (1 Jul 1646 - 14 Nov 1716)   [  German  ]

$\mathcal{J}$acob   $\mathscr{B}$ernoulli (6 Jan 1655 - 16 Aug 1705)   [  Swiss | Basel  ]

$\mathscr{A}$braham de $\mathscr{M}$oivre   (26 May 1667 - 27 November 1754)   [  French  ]

$\mathcal{J}$ohann   $\mathscr{B}$ernoulli (6 Aug 1667 - 1 Jan 1748)   [  Swiss | Basel  ]

$\mathcal{B}$rook   $\mathcal{T}$aylor (18 August 1685 - 29 Dec 1731)   [  British  ]

$\mathcal{C}$olin   $\mathcal{M}$aclaurin (Feb 1695 - 14 Jun 1746)   [  Scottish  ]

$\mathcal{D}$aniel   $\mathscr{B}$ernoulli (8 Feb 1700 - 27 Mar 1782)   [  Swiss | Basel  ]

$\mathfrak{L}$eonard   $\mathfrak{E}$uler   (15 Apr 1707 – 18 Sept 1783)   [  Switzerland  ]

$\mathcal{I}$mmanuel   $\mathcal{K}$ant   (22 April 1724 – 12 Feb 1804)   [  Britain  ]

$\mathscr{J}$oseph   $\mathscr{L}$ouis   $\mathscr{L}$agrange   (25 Jan 1736 – 10 Apr 1813)   [  France  ]

$\mathscr{C}$harles-$\mathscr{A}$ugustin de $\mathscr{C}$oulomb   (14 Jun 1736 - 23 Aug 1806)   [  French  ]

$\mathscr{A}$ntoine-$\mathscr{L}$aurent de $\mathscr{L}$avoisier   (26 Aug 1743 - 8 May 1794)   [  French  ]

$\mathscr{A}$lessandro   $\mathscr{G}$iuseppe   $\mathscr{A}$ntonio   $\mathscr{V}$olta   (18 Feb 1745 - 5 March 1827)   [  Italian  ]

$\mathscr{P}$ierre-$\mathscr{S}$imon $\mathcal{M}$arquis de $\mathcal{L}$aplace (23 Mar 1749 - 5 Mar 1827)   [  French  ]

$\mathscr{J}$ean-$\mathscr{B}$aptiste   $\mathscr{J}$oseph   $\mathscr{F}$ourier   (21 Mar 1768 - 16 May 1830)   [  British  ]

$\mathcal{T}$homas   $\mathcal{Y}$oung   (13 Jun 1773 - 10 May 1829)   [  British  ]

$\mathscr{A}$ndré-$\mathscr{M}$arie   $\mathscr{A}$mpere   (20 Jan 1775 - 10 June 1836)   [  French  ]

$\mathscr{L}$orenzo   $\mathscr{R}$omano   $\mathscr{A}$medeo   $\mathscr{C}$arlo   $\mathscr{A}$vogadro   (9 Aug 1776 - 9 Jul 1856)   [  Italian  ]

$\mathbb{C}$arl   $\mathbb{F}$rederich   $\mathbb{G}$au$\beta$   (30 Apr 1777 - 23 Feb 1855)   [  Prussia  ]

$\mathscr{S}$imeon   $\mathscr{D}$enis   $\mathscr{P}$oisson   (21 Jun 1781 - 25 Apr 1840)   [  French  ]

$\mathscr{J}$acques   $\mathscr{P}$hilippe   $\mathscr{M}$arie   $\mathscr{B}$inet   (2 Feb 1786 – 12 May 1856)   [  France  ]

$\mathcal{G}$eorge   $\mathcal{S}$imon   $\mathcal{O}$hm   (16 Mar 1789 - 6 Jul 1854)   [  German  ]

$\mathscr{A}$ugustine-$\mathscr{L}$ouis   $\mathscr{C}$auchy   (21 August 1789 – 23 May 1857)   [  French  ]

$\mathcal{N}$ikolai   $\mathcal{I}$vanovich $\mathcal{L}$obachevsky (1 Dec 1792 - 24 Feb 1856)   [  Russian  ]

$\mathcal{G}$eorge   $\mathcal{G}$reen (14 Jul 1793 - 31 May 1841)   [  British  ]

$\mathcal{M}$ichael   $\mathcal{F}$araday (22 Sep 1797 - 25 Aug 1867)   [  British  ]

$\mathfrak{J}$anós   $\mathfrak{B}$olyaí   (15 Dec 1802 – 27 Jan 1860)   [  Hungary  ]

$\mathbb{N}$iels   $\mathbb{H}$endrik   $\mathbb{A}$bel   (5 Aug 1802 - 6 Apr 1829)   [  Norwegian  ]

$\mathcal{J}$oseph   $\mathcal{L}$iouville   (24 March 1809 -8 Sep 1882)   [  French  ]

$\mathscr{E}$varisté   $\mathscr{G}$alois   (25 Oct 1811 – 31 May 1832)   [  France  ]

$\mathscr{P}$ierre   $\mathscr{A}$lphonse   $\mathscr{L}$aurent (18 Jul 1813 - 2 Sep 1854)   [  French  ]

$\mathcal{G}$eorge   $\mathcal{B}$oolos   (2 Nov 1815 - 8 Dec 1864)   [  Britain  ]

$\mathcal{K}$arl   $\mathcal{W}$eierstra$\beta$   (31 Oct 1815 - 19 Feb 1897)   [  German  ]

$\mathcal{J}$ames   $\mathcal{P}$rescot   $\mathcal{J}$oule   (24 Dec 1818 - 11 Oct 1889)   [  British  ]

$\mathcal{G}$eorge   $\mathcal{S}$tokes   (13 Aug 1819 - 1 Feb 1903)   [  Irish  ]

$\mathcal{A}$rthur   $\mathcal{C}$ayley   (16 Aug 1821 - 26 Jan 1895)   [  Britain  ]

$\mathcal{G}$ustav   $\mathcal{R}$obert   $\mathcal{K}$irchoff   (12 March 1824 - 17 Oct 1887)   [  German  ]

$\mathcal{G}$eorge   $\mathcal{F}$rederich   $\mathcal{B}$ernard   $\mathcal{R}$iemann   (17 Sept 1826 - 20 Jul 1866)   [  German  ]

$\mathcal{J}$ames   $\mathcal{C}$lerk   $\mathcal{M}$axwell (13 Jun 1831 - 5 Nov 1879)   [  Scottish  ]

$\mathcal{J}$ulius   $\mathcal{W}$ilhelm   $\mathcal{R}$ichard   $\mathcal{D}$edekind   (6 Oct 1831 – 12 Feb 1916)   [  German  ]

$\mathcal{C}$harles   $\mathcal{L}$utwidge   $\mathcal{D}$odgson (27 Jan 1832 – 14 Jan 1898)   [  British  ]

$\mathcal{D}$mitri   $\mathcal{I}$vanovich   $\mathcal{M}$endeleev   (8 Feb 1834 - 2 Feb 1907)   [  Russian  ]

$\mathscr{M}$arie   $\mathscr{E}$nnemond   $\mathscr{C}$amille   $\mathcal{J}$ordan (5 Jan 1838 - 22 Jan 1922)   [  French  ]

$\mathcal{C}$harles   $\mathcal{S}$anders   $\mathcal{P}$ierce   (10 Sep 1839 - 19 Apr 1914)   [  American  ]

$\mathcal{G}$eorge   $\mathcal{C}$antor   (3 March 1845 - 6 Jan 1918)   [  George  ]

$\mathcal{T}$homas   $\mathcal{A}$lva   $\mathcal{E}$dison   (11 Feb 1847 - 18 Oct 1831)   [  American  ]

$\mathcal{A}$lexander   $\mathcal{G}$raham   $\mathcal{B}$ell   (3 March 1847 - 2 Aug 1922)   [  Scottish American  ]

$\mathcal{F}$rederich   $\mathcal{L}$udwig   $\mathcal{G}$otlob   $\mathcal{F}$rege   (8 Nov 1848 - 26 July 1925)   [  German  ]

$\mathcal{J}$ohn   $\mathcal{A}$mbrose   $\mathcal{F}$lemming   (29 Nov 1849 - 18 Apr 1945)   [  British  ]

$\mathcal{O}$liver   $\mathcal{H}$eaviside   (18 May 1850 - 3 Feb 1925)   [  British  ]

$\mathcal{H}$endrik   $\mathcal{A}$ntoon   $\mathcal{L}$orentz   (18 Jul 1853 - 4 Feb 1928)   [  Dutch  ]

$\mathcal{J}$ules   $\mathcal{H}$enri   $\mathcal{P}$oincaré   (29 Apr 1854 - 17 Jul 1912)   [  French  ]

$\mathcal{J}$ohannes   $\mathcal{R}$obert   $\mathcal{R}$ydberg   (8 Nov 1854 - 28 Dec 1919)   [  Swedish  ]

$\mathcal{N}$iels   $\mathcal{H}$endrik   $\mathcal{D}$avid   $\mathcal{B}$ohr   (7 Oct 1855 - 18 Nov 1962)   [  Danish  ]

$\mathcal{N}$ikola   $\mathcal{T}$esla (10 Jul 1856 - 7 Jan 1943)   [  Serbian+American  ]

$\mathcal{J}$oseph   $\mathcal{J}$ohn   $\mathcal{T}$homson   (18 Dec 1856 - 30 Aug 1940)   [  British  ]

$\mathcal{H}$einrich   $\mathcal{R}$udolf   $\mathcal{H}$ertz   (22 Feb 1857 - 1 Jan 1894)   [  German  ]

$\mathcal{M}$ax   $\mathcal{K}$arl   $\mathcal{E}$rnst   $\mathcal{L}$udwig   $\mathcal{P}$lanck   (23 Apr 1858 - 4 Oct 1947)   [  German  ]

$\mathcal{G}$iuseppe   $\mathcal{P}$eano   [dʒuˈzɛppe / peˈɑːnoʊ;]   (27 Aug 1858 - 20 Apr 1932)   [  Italian  ]

$\mathcal{A}$lfred   $\mathcal{N}$orth   $\mathcal{W}$hitehead   (15 Feb 1861 - 30 Dec 1947)   [  British  ]

$\mathcal{R}$obert   $\mathcal{A}$ndrews   $\mathcal{M}$illikan   (22 March 1868 - 19 Dec 1953)   [  American  ]

$\mathcal{D}$avid   $\mathcal{H}$ilbert   (23 Jan 1862 - 14 Feb 1943)   [  German  ]

$\mathcal{H}$erman   $\mathcal{M}$inkowski   (22 Jun 1864 - 12 Jan 1909)   [  German  ]

$\mathcal{F}$elix   $\mathcal{H}$ausdorff   (8 Nov 1868 - 26 Jan 1942)   [  German  ]

$\mathcal{E}$rnest   $\mathcal{R}$utherford   (30 Aug 1871 - 19 Oct 1937)   [  New Zealand  ]

$\mathcal{B}$ertrand   $\mathcal{R}$ussel   (18 May 1872 - 2 Feb 1970)   [  British  ]

$\mathcal{A}$lbert   $\mathcal{E}$instein   (14 March 1879 - 18 Apr 1955)   [  German  ]

$\mathcal{H}$ans   $\mathcal{H}$ahn   (27 Sep 1879 – 24 July 1934)   [  Austrian  ]

$\mathcal{F}$rigyes   $\mathcal{R}$iesz   (22 Jan 1880 - 28 Feb 1956)   [  Hungarian  ]

$\mathcal{J}$ulius   $\mathcal{E}$dgar   $\mathcal{E}$Lilienfeld   (18 Apr 1882 - 28 Aug 1963)   [  Austro-Hungarian American  ]

$\mathcal{E}$rwin   $\mathcal{R}$udolf   $\mathcal{J}$osef   $\mathcal{A}$lexander   $\mathcal{S}$chro¨dinger   (12 Aug 1887 - 4 Jan 1961)   [  German  ]

$\mathcal{M}$oses   $\mathcal{I}$lyich   $\mathcal{S}$chönfinkel   (29 Sep 1888 - 1942)   [  Russian  ]

$\mathcal{S}$tefan   $\mathcal{B}$anach(30 March 1892 – 31 Aug 1945)   [  Polish  ]

$\mathcal{K}$azimierz   $\mathcal{K}$uratowski   (2 Feb 1896 - 18 Jun 1980)   [  Polish  ]

$\mathcal{H}$enry   $\mathcal{M}$aurice   $\mathcal{S}$heffer   (1 Sep 1882 - 17 Mar 1964)   [  Jewish Ukranian American  ]

$\mathcal{J}$ames   $\mathcal{C}$hadwick   (20 Oct 1891 - 24 Jul 1974)   [  British  ]

$\mathscr{L}$ouis   $\mathscr{V}$ictor   $\mathscr{P}$ierre   $\mathscr{R}$aymond de $\mathscr{B}$roglie   (15 Aug 1892 - 19 March 1987)   [  French  ]

$\mathcal{E}$mil   $\mathcal{L}$eon   $\mathcal{P}$ost   (11 Feb 1897 - 21 Apr 1954)   [  American  ]

$\mathcal{W}$olfgang   $\mathcal{E}$rnst   $\mathcal{P}$auli   (25 Apr 1900 - 15 Dec 1958)   [  Austrian  ]

$\mathcal{H}$askell   $\mathcal{C}$urry   (12 Sep 1900 - 1 Sep 1982)   [  American  ]

$\mathcal{W}$erner   $\mathcal{K}$arl   $\mathcal{H}$eisenberg   (5 Dec 1901 - 1 Feb 1976)   [  German  ]

$\mathcal{A}$lfred   $\mathcal{T}$arski   (14 Jan 1901 - 26 Oct 1983)   [  Polish American  ]

$\mathcal{W}$alter   $\mathcal{H}$ouser   $\mathcal{B}$rattain   (10 Feb 1902 - 13 Oct 1987)   [  American  ]

$\mathcal{A}$lonzo   $\mathcal{C}$hurch   (14 June 1903 - 11 August 1995)   [  American  ]

$\mathcal{A}$dolf   $\mathcal{L}$indenbaum   (12 June 1904 – August 1941)   [  Polish+Jewish  ]

$\mathcal{R}$ózsa   $\mathcal{P}$éter   (17 Feb 1905 - 16 Feb 1977)   [  Hungarian  ]

$\mathcal{K}$urt   $\mathcal{F}$rederich   $\mathcal{G}$ödel   [kʊʁt ˈɡøːdl]̩   (1906 April 28 – 14 January 1978)   [  German  ]

$\mathcal{M}$ax   $\mathcal{A}$ugust   $\mathcal{Z}$orn   (6 June 1906 – 9 March 1993)   [  German  ]

$\mathcal{J}$ohn   $\mathcal{B}$arkley   $\mathcal{R}$osser (6 Dec 1907 - 5 Sep 1989)   [  American  ]

$\mathcal{V}$ictor   $\mathcal{I}$vanovich   $\mathcal{S}$hestakov   (1907 - 1987)   [  Russian  ]

$\mathcal{A}$kira   $\mathcal{N}$akashima   中島 章   (5 Jan 1908 - 29 Oct 1970)   [  Japanese  ]

$\mathscr{J}$acques   $\mathcal{H}$erbrand (12 Feb 1908 - 27 Jul 1931)   [  French  ]

$\mathcal{J}$ohn   $\mathcal{B}$ardeen   (23 May 1908 - 30 Jan 1991)   [  American  ]

$\mathcal{S}$tephen   $\mathcal{C}$ole   $\mathcal{K}$leene   (5 Jan 1909 - 25 Jan 1994)   [  American  ]

$\mathcal{G}$erhard   $\mathcal{K}$arl   $\mathcal{E}$nrich   $\mathcal{G}$entzen   (24 Nov 1909 – 4 Aug 1945)   [  German  ]

$\mathcal{W}$illiam   $\mathcal{B}$radford   $\mathcal{S}$hockley   (13 Feb 1910 - 12 Aug 1989)   [  American  ]

$\mathcal{A}$lan   $\mathcal{M}$athison   $\mathcal{T}$uring   (23 Jun 1912 - 7 Jun 1954)   [  British  ]

$\mathcal{C}$laude   $\mathcal{E}$lwood   $\mathcal{S}$hannon   (30 Apr 1916 - 24 Feb 2001)   [  American  ]

$\mathcal{M}$ohamed   $\mathcal{A}$talla   محمد عطاالله   (4 August 1924 - 30 Dec 2009)   [  Egyptian American  ]

$\mathcal{E}$dsger   $\mathcal{W}$ybe   $\mathcal{D}$ijkstra (11 May 1930 - 6 August 2002)   [  Dutch  ]

$\mathcal{D}$awon   $\mathcal{K}$ahng   강대원   (4 May 1931 - 13 May 1992)   [  Korean American  ]

$\mathcal{A}$rthur   $\mathcal{J}$ohn   $\mathcal{R}$obin   $\mathcal{G}$orell   $\mathcal{M}$ilner   (13 Jan 1934 – 20 Mar 2010)   [  British  ]

$\mathcal{R}$ichard   $\mathcal{E}$arl   $\mathcal{H}$odel   (1938 – present)   [  American  ]

$\mathcal{S}$aul   $\mathcal{A}$aron   $\mathcal{K}$ripke   (13 Nov 1940 – 15 Sep 2022)   [  American  ]

$\mathcal{D}$ana   $\mathcal{S}$cott   (11 Oct 1932)   [  American  ]

$\mathcal{J}$ohn von $\mathcal{N}$eumann   (15 Mar 1955 - 8 Feb 1957)   [  Hungarian American  ]

$\mathcal{M}$atthew   $\mathcal{H}$ennesy   (1990)   [  Irish  ]

$\mathcal{E}$rnst   $\mathcal{F}$redrich   $\mathcal{F}$erdinand   $\mathcal{Z}$ermelo   (27 Jul 1871 - 21 May 1953)   [  German  ]

$\mathcal{A}$dolf   $\mathcal{A}$braham   $\mathcal{H}$alevi   $\mathcal{F}$raenkel   (17 Feb 1891 - 15 Oct 1965)   אברהם הלוי (אדולף) פרנקל   [  German Israeli  ]